Introduction
Developing and validating psychological measures requires examining their psychometric properties, including their reliability and validity. One aspect of a measure’s validity is its item difficulty, which refers to how easy or difficult each individual item is for respondents to answer correctly. Another important aspect is item discrimination, which measures the extent to which each item distinguishes between participants who have high or low levels of the construct being measured.
Understanding item difficulty and item discrimination is crucial for several reasons. First, items that are too easy or too difficult can limit the variability of responses, making it harder to discriminate between participants who have different levels of the construct being measured. Second, items with low discrimination may not effectively differentiate between participants with different levels of the construct, leading to decreased validity.
In this blog post, we’ll explore how to calculate item difficulty and item discrimination in R using an example dataset. We’ll explain what each of these psychometric properties are, why they’re important, and how to interpret the results. We’ll also discuss some limitations and considerations when examining these properties. So let’s get started!
The dataset is generated via this web application based on Item Response Theory 2-Parameter Logistic Model. The dataset consists of randomly generated 40 items with a sample size of 500. The a-parameters of the items vary between 0.8 and 1.3 while b-parameters vary between -3 and 3. The c and d parameters are fixed to 0 and 1 respectively for all items.
Here are the package(s) we use in this post:
Item Difficulty
Item difficulty is a psychometric property that measures how easy or difficult an item is for respondents to answer correctly. Examining item difficulty is important because it can help identify items that are too easy or too difficult, which can limit the variability of responses and make it harder to discriminate between participants who have different levels of the construct being measured.
The proportion of correct responses for each item is calculated and reported as the item difficulty value. This calculation can be done manually using spreadsheet software or programmatically using statistical software such as R or SPSS. R has many packages and functions out there that we can use to calculate item difficulties. Yet we will calculate them simply with colMeans() function.
Let’s start by introducing the dataset to R environment.
my_data<-read.csv("data for post about item difficulty and discrimination.csv",sep=";", header = TRUE)
head(my_data) i1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i11 i12 i13 i14 i15 i16 i17 i18 i19 i20 i21
1 0 1 1 1 0 0 1 0 0 1 1 0 1 1 1 1 0 0 0 0 0
2 0 1 1 1 0 0 1 0 0 1 0 0 1 0 1 1 1 1 0 1 0
3 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0
4 1 1 0 0 0 0 0 0 0 1 0 0 1 1 0 1 1 0 0 0 0
5 0 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0
6 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 0 0 1
i22 i23 i24 i25 i26 i27 i28 i29 i30 i31 i32 i33 i34 i35 i36 i37 i38 i39 i40
1 0 0 1 1 1 0 1 0 0 0 1 0 1 0 1 0 1 1 0
2 0 0 1 1 1 0 0 0 0 0 0 1 1 0 1 0 0 1 1
3 0 0 1 1 1 0 1 0 0 0 1 1 1 1 1 0 1 1 1
4 0 0 0 1 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1
5 0 0 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 1 1
6 0 0 1 1 1 0 1 1 0 0 1 1 1 1 1 1 1 1 1Now let’s get the item difficulties:
# Calculate item difficulty
item_difficulty <- colMeans(my_data)
item_difficulty i1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i11 i12 i13
0.212 0.918 0.910 0.782 0.112 0.394 0.742 0.400 0.862 0.870 0.774 0.386 0.882
i14 i15 i16 i17 i18 i19 i20 i21 i22 i23 i24 i25 i26
0.682 0.594 0.928 0.722 0.384 0.174 0.346 0.512 0.176 0.100 0.682 0.900 0.882
i27 i28 i29 i30 i31 i32 i33 i34 i35 i36 i37 i38 i39
0.264 0.536 0.148 0.044 0.046 0.918 0.638 0.946 0.610 0.800 0.146 0.566 0.928
i40
0.952 Interpreting the results of item difficulty is straightforward. Items with higher difficulty values indicate that they were easier for participants to answer correctly, while items with lower difficulty values were more difficult. In our example dataset, the output shows that item 40 had the highest difficulty value of 0.952, meaning that 95.2% of participants answered this item correctly. Item 30, on the other hand, had the lowest difficulty value of 0.044, meaning that only 4.4% of participants answered this item correctly.
It’s important to note that each construct should be evaluated within its own concept while interpreting item difficulties. Yet, for achievement tests, a generic classification might be defined as “easy” if the index is 0.85 or above; “moderate” if it is between 0.41 and 0.84; and “hard” if it is 0.40 or below. Also, item difficulty is not the only factor to consider when evaluating the quality of a measure. Items that are too easy or too difficult may still be valid and reliable, depending on the construct being measured and the purpose of the measure. However, examining item difficulty can provide valuable insights into the psychometric properties of the measure and inform decisions about item selection and revision.
Item Discrimination
Item discrimination is another important psychometric property that measures the extent to which each item differentiates between participants who have high or low levels of the construct being measured. It indicates how well an item distinguishes between participants with different levels of the construct.
It’s important to note that (just like item difficulties) each construct should be evaluated within its own concept while interpreting item discriminations. Yet, for achievement tests, a generic classification might be defined as “good” if the index is above 0.30; “fair” if it is between 0.10 and 0.30; and “poor” if it is below 0.10.
To obtain a value for item discrimination, there are several statistical approaches that we can utilize. Here we will discuss (1) correlation between item and total score with the item, (2) correlation between item and total score without the item, and (3) upper-lower groups index.
1. Correlation between item and total score with the item
This approach is based on calculating the point-biserial correlation coefficient (rpb) between each item and the total score of the measure. The total score is calculated by summing the scores of all items. The rpb ranges from -1 to 1, with values closer to 1 indicating higher discrimination.
Let’s first calculate the total score for each participant in our example dataset. Then, use a for loop to calculate rpb coefficients for each item:
#get the total score for each participant
total_score <- rowSums(my_data)
#There are 40 items in the test:
item_discrimination1 <- 40
#calculate rpb for each item:
for(i in 1:40){
item_discrimination1[i] <- cor(total_score, my_data[,i])
}
round(item_discrimination1,4) [1] 0.3984 0.2162 0.2308 0.4485 0.3019 0.4847 0.4148 0.4548 0.2796 0.3335
[11] 0.4498 0.5138 0.2735 0.4336 0.4423 0.1956 0.4288 0.4133 0.3297 0.4214
[21] 0.4909 0.3174 0.3222 0.4098 0.3312 0.3464 0.3737 0.4876 0.2481 0.2257
[31] 0.1783 0.3536 0.4094 0.2837 0.3893 0.3888 0.3962 0.5025 0.2866 0.19062. Correlation between item and total score without the item
This approach is very similar to the first one. The only difference is that when we calculate the correlation between an item and the total score, we do not include the item. This type of an approach will result in slightly reduced index values when compared to the first approach. Therefore, it is usually a more-preferred approach by test developers (we would love to stay in the safe-zone).
The package multilevel has a specific function for this index. The item.total() function takes only the dataset as input and provides us with a dataframe with four columns: item name, discrimination index, a reliability index without the item and the sample size. Yet, we only need the discrimination index. Here how we get it:
item_discrimination2<-multilevel::item.total(my_data)
item_discrimination2$Item.Total [1] 0.3365024 0.1703597 0.1832279 0.3887597 0.2511883 0.4160659 0.3493047
[8] 0.3837360 0.2232991 0.2803945 0.3892913 0.4477891 0.2207879 0.3648121
[15] 0.3701690 0.1521115 0.3624807 0.3399690 0.2694241 0.3503333 0.4211616
[22] 0.2564267 0.2746220 0.3395723 0.2838892 0.2959223 0.3053936 0.4177549
[29] 0.1892085 0.1916937 0.1429237 0.3110586 0.3368093 0.2471547 0.3143658
[36] 0.3277659 0.3428951 0.4342855 0.2447900 0.15461143. Upper-lower groups index
Personally, I feel that this approach is the most meaningfully-related approach in terms of “discrimination”. That’s because while calculating it, we divide the whole group into sub-groups (usually three groups) according to their total scores. Then, we calculate the discrimination index for an item by comparing these groups’ responses to that item. This definition feels more like a discrimination index to my illiterate ears.
In R environment, ShinyItemAnalysis package has a specific function for this index. The gDiscrim() function has several arguements such as Data(the data set), k (the number of sub groups and 3 is default), l and u (numeric values to define the lower and upper groups and the defaults are 1 and 3 consecutively). There are other arguments that should be checked on the manual before using the function.
We simply use the function as:
item_discrimination3<-ShinyItemAnalysis::gDiscrim(my_data)
item_discrimination3 i1 i2 i3 i4 i5 i6 i7
0.35177700 0.11253051 0.12801251 0.42537370 0.20042709 0.57908786 0.40470561
i8 i9 i10 i11 i12 i13 i14
0.56204240 0.19718578 0.26586333 0.43982611 0.56566504 0.21888347 0.50640635
i15 i16 i17 i18 i19 i20 i21
0.49603417 0.11253051 0.45530811 0.44428768 0.26346095 0.46442190 0.56829622
i22 i23 i24 i25 i26 i27 i28
0.26449054 0.20145668 0.43875839 0.20908328 0.25709274 0.36420836 0.59567572
i29 i30 i31 i32 i33 i34 i35
0.17720409 0.08419768 0.07748627 0.19100824 0.45732916 0.12957596 0.41599298
i36 i37 i38 i39 i40
0.37633466 0.29804759 0.54766626 0.13163514 0.09601891 Note that if you change the number of subgroups, you should be careful while interpreting the results.
No matter what statistical approach you use to estimate discrimination indexes, it’s also important to note that item discrimination can be influenced by factors such as the sample size, the range of scores, and the homogeneity of the sample. Therefore, it’s recommended to examine item discrimination in conjunction with other psychometric properties such as item difficulty and reliability.
A Package of Personal Preferrance
While we can calculate both difficulty and discrimination indexes manually or by using different functions from different packages, my totally-subjective opinion is that ItemAnalysis() function from the ShinyItemAnalysis package gives a well-groomed output for many item statistics. The following code snippet simply provides us with many indexes including difficulty and three types of discrimination indexes:
#round is for rounding the values in the results.
item_stats<-round(ShinyItemAnalysis::ItemAnalysis(my_data),2)
#to see all the output in a table:
knitr::kable(item_stats)| Difficulty | Mean | SD | Cut.score | obs.min | Min.score | obs.max | Max.score | Prop.max.score | RIR | RIT | Corr.criterion | ULI | gULI | Alpha.drop | Index.rel | Index.val | Perc.miss | Perc.nr | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | 0.21 | 0.21 | 0.41 | NA | 0 | 0 | 1 | 1 | 0.21 | 0.34 | 0.40 | NA | 0.35 | NA | 0.83 | 0.16 | NA | 0 | 0 |
| i2 | 0.92 | 0.92 | 0.27 | NA | 0 | 0 | 1 | 1 | 0.92 | 0.17 | 0.22 | NA | 0.11 | NA | 0.84 | 0.06 | NA | 0 | 0 |
| i3 | 0.91 | 0.91 | 0.29 | NA | 0 | 0 | 1 | 1 | 0.91 | 0.18 | 0.23 | NA | 0.13 | NA | 0.84 | 0.07 | NA | 0 | 0 |
| i4 | 0.78 | 0.78 | 0.41 | NA | 0 | 0 | 1 | 1 | 0.78 | 0.39 | 0.45 | NA | 0.43 | NA | 0.83 | 0.19 | NA | 0 | 0 |
| i5 | 0.11 | 0.11 | 0.32 | NA | 0 | 0 | 1 | 1 | 0.11 | 0.25 | 0.30 | NA | 0.20 | NA | 0.84 | 0.10 | NA | 0 | 0 |
| i6 | 0.39 | 0.39 | 0.49 | NA | 0 | 0 | 1 | 1 | 0.39 | 0.42 | 0.48 | NA | 0.58 | NA | 0.83 | 0.24 | NA | 0 | 0 |
| i7 | 0.74 | 0.74 | 0.44 | NA | 0 | 0 | 1 | 1 | 0.74 | 0.35 | 0.41 | NA | 0.40 | NA | 0.83 | 0.18 | NA | 0 | 0 |
| i8 | 0.40 | 0.40 | 0.49 | NA | 0 | 0 | 1 | 1 | 0.40 | 0.38 | 0.45 | NA | 0.56 | NA | 0.83 | 0.22 | NA | 0 | 0 |
| i9 | 0.86 | 0.86 | 0.35 | NA | 0 | 0 | 1 | 1 | 0.86 | 0.22 | 0.28 | NA | 0.20 | NA | 0.84 | 0.10 | NA | 0 | 0 |
| i10 | 0.87 | 0.87 | 0.34 | NA | 0 | 0 | 1 | 1 | 0.87 | 0.28 | 0.33 | NA | 0.27 | NA | 0.83 | 0.11 | NA | 0 | 0 |
| i11 | 0.77 | 0.77 | 0.42 | NA | 0 | 0 | 1 | 1 | 0.77 | 0.39 | 0.45 | NA | 0.44 | NA | 0.83 | 0.19 | NA | 0 | 0 |
| i12 | 0.39 | 0.39 | 0.49 | NA | 0 | 0 | 1 | 1 | 0.39 | 0.45 | 0.51 | NA | 0.57 | NA | 0.83 | 0.25 | NA | 0 | 0 |
| i13 | 0.88 | 0.88 | 0.32 | NA | 0 | 0 | 1 | 1 | 0.88 | 0.22 | 0.27 | NA | 0.22 | NA | 0.84 | 0.09 | NA | 0 | 0 |
| i14 | 0.68 | 0.68 | 0.47 | NA | 0 | 0 | 1 | 1 | 0.68 | 0.36 | 0.43 | NA | 0.51 | NA | 0.83 | 0.20 | NA | 0 | 0 |
| i15 | 0.59 | 0.59 | 0.49 | NA | 0 | 0 | 1 | 1 | 0.59 | 0.37 | 0.44 | NA | 0.50 | NA | 0.83 | 0.22 | NA | 0 | 0 |
| i16 | 0.93 | 0.93 | 0.26 | NA | 0 | 0 | 1 | 1 | 0.93 | 0.15 | 0.20 | NA | 0.11 | NA | 0.84 | 0.05 | NA | 0 | 0 |
| i17 | 0.72 | 0.72 | 0.45 | NA | 0 | 0 | 1 | 1 | 0.72 | 0.36 | 0.43 | NA | 0.46 | NA | 0.83 | 0.19 | NA | 0 | 0 |
| i18 | 0.38 | 0.38 | 0.49 | NA | 0 | 0 | 1 | 1 | 0.38 | 0.34 | 0.41 | NA | 0.44 | NA | 0.83 | 0.20 | NA | 0 | 0 |
| i19 | 0.17 | 0.17 | 0.38 | NA | 0 | 0 | 1 | 1 | 0.17 | 0.27 | 0.33 | NA | 0.26 | NA | 0.84 | 0.13 | NA | 0 | 0 |
| i20 | 0.35 | 0.35 | 0.48 | NA | 0 | 0 | 1 | 1 | 0.35 | 0.35 | 0.42 | NA | 0.46 | NA | 0.83 | 0.20 | NA | 0 | 0 |
| i21 | 0.51 | 0.51 | 0.50 | NA | 0 | 0 | 1 | 1 | 0.51 | 0.42 | 0.49 | NA | 0.57 | NA | 0.83 | 0.25 | NA | 0 | 0 |
| i22 | 0.18 | 0.18 | 0.38 | NA | 0 | 0 | 1 | 1 | 0.18 | 0.26 | 0.32 | NA | 0.26 | NA | 0.84 | 0.12 | NA | 0 | 0 |
| i23 | 0.10 | 0.10 | 0.30 | NA | 0 | 0 | 1 | 1 | 0.10 | 0.27 | 0.32 | NA | 0.20 | NA | 0.84 | 0.10 | NA | 0 | 0 |
| i24 | 0.68 | 0.68 | 0.47 | NA | 0 | 0 | 1 | 1 | 0.68 | 0.34 | 0.41 | NA | 0.44 | NA | 0.83 | 0.19 | NA | 0 | 0 |
| i25 | 0.90 | 0.90 | 0.30 | NA | 0 | 0 | 1 | 1 | 0.90 | 0.28 | 0.33 | NA | 0.21 | NA | 0.83 | 0.10 | NA | 0 | 0 |
| i26 | 0.88 | 0.88 | 0.32 | NA | 0 | 0 | 1 | 1 | 0.88 | 0.30 | 0.35 | NA | 0.26 | NA | 0.83 | 0.11 | NA | 0 | 0 |
| i27 | 0.26 | 0.26 | 0.44 | NA | 0 | 0 | 1 | 1 | 0.26 | 0.31 | 0.37 | NA | 0.36 | NA | 0.83 | 0.16 | NA | 0 | 0 |
| i28 | 0.54 | 0.54 | 0.50 | NA | 0 | 0 | 1 | 1 | 0.54 | 0.42 | 0.49 | NA | 0.60 | NA | 0.83 | 0.24 | NA | 0 | 0 |
| i29 | 0.15 | 0.15 | 0.36 | NA | 0 | 0 | 1 | 1 | 0.15 | 0.19 | 0.25 | NA | 0.18 | NA | 0.84 | 0.09 | NA | 0 | 0 |
| i30 | 0.04 | 0.04 | 0.21 | NA | 0 | 0 | 1 | 1 | 0.04 | 0.19 | 0.23 | NA | 0.08 | NA | 0.84 | 0.05 | NA | 0 | 0 |
| i31 | 0.05 | 0.05 | 0.21 | NA | 0 | 0 | 1 | 1 | 0.05 | 0.14 | 0.18 | NA | 0.08 | NA | 0.84 | 0.04 | NA | 0 | 0 |
| i32 | 0.92 | 0.92 | 0.27 | NA | 0 | 0 | 1 | 1 | 0.92 | 0.31 | 0.35 | NA | 0.19 | NA | 0.83 | 0.10 | NA | 0 | 0 |
| i33 | 0.64 | 0.64 | 0.48 | NA | 0 | 0 | 1 | 1 | 0.64 | 0.34 | 0.41 | NA | 0.46 | NA | 0.83 | 0.20 | NA | 0 | 0 |
| i34 | 0.95 | 0.95 | 0.23 | NA | 0 | 0 | 1 | 1 | 0.95 | 0.25 | 0.28 | NA | 0.13 | NA | 0.84 | 0.06 | NA | 0 | 0 |
| i35 | 0.61 | 0.61 | 0.49 | NA | 0 | 0 | 1 | 1 | 0.61 | 0.31 | 0.39 | NA | 0.42 | NA | 0.83 | 0.19 | NA | 0 | 0 |
| i36 | 0.80 | 0.80 | 0.40 | NA | 0 | 0 | 1 | 1 | 0.80 | 0.33 | 0.39 | NA | 0.38 | NA | 0.83 | 0.16 | NA | 0 | 0 |
| i37 | 0.15 | 0.15 | 0.35 | NA | 0 | 0 | 1 | 1 | 0.15 | 0.34 | 0.40 | NA | 0.30 | NA | 0.83 | 0.14 | NA | 0 | 0 |
| i38 | 0.57 | 0.57 | 0.50 | NA | 0 | 0 | 1 | 1 | 0.57 | 0.43 | 0.50 | NA | 0.55 | NA | 0.83 | 0.25 | NA | 0 | 0 |
| i39 | 0.93 | 0.93 | 0.26 | NA | 0 | 0 | 1 | 1 | 0.93 | 0.24 | 0.29 | NA | 0.13 | NA | 0.84 | 0.07 | NA | 0 | 0 |
| i40 | 0.95 | 0.95 | 0.21 | NA | 0 | 0 | 1 | 1 | 0.95 | 0.15 | 0.19 | NA | 0.10 | NA | 0.84 | 0.04 | NA | 0 | 0 |
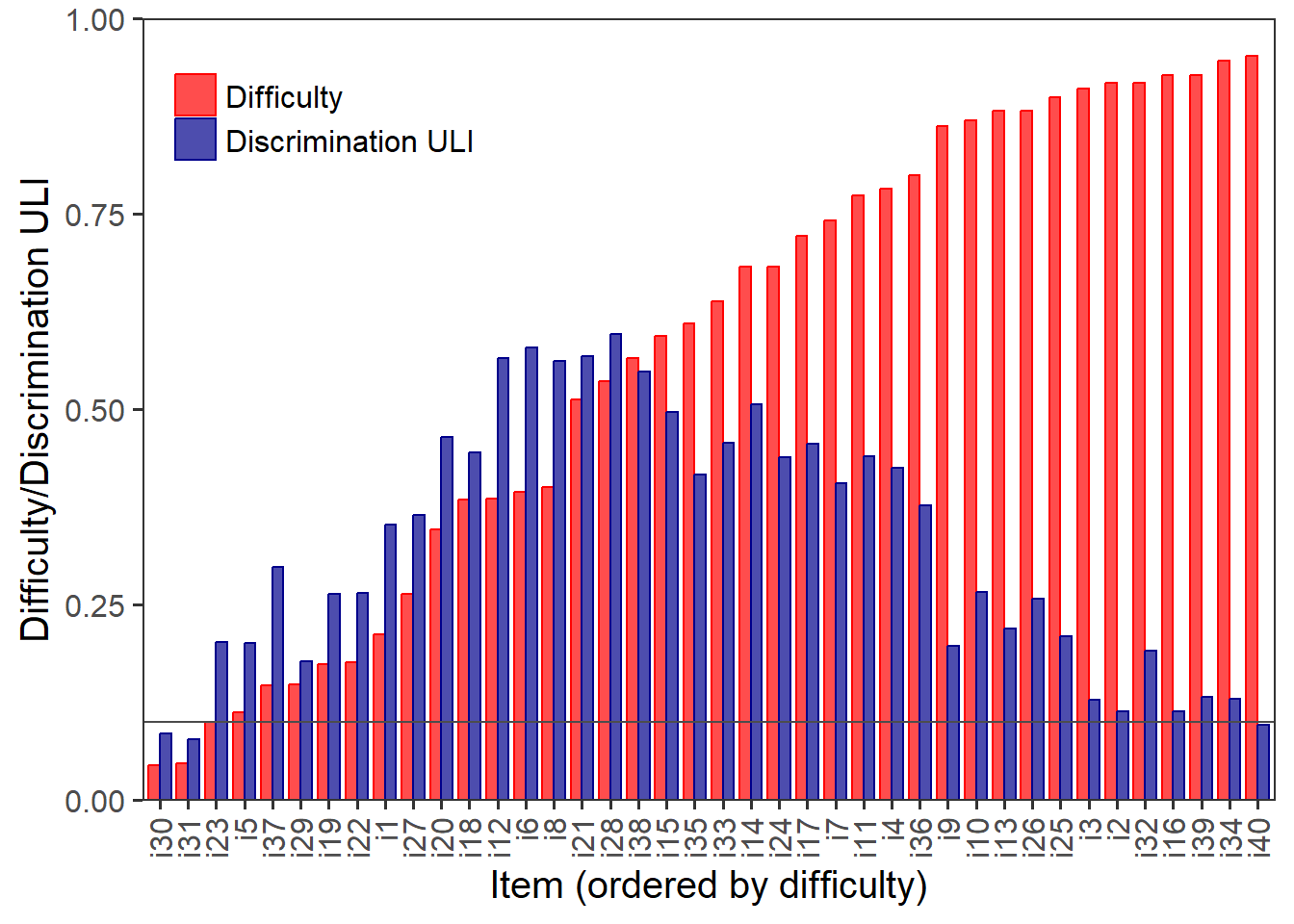
The same package also provides us with a nice visualization function (DDplot) for item difficulty and discrimination of any approach stated above. It takes discrim argument that can be defined as RIT (the first approach), RIR (the second approach above) or ULI (the third approach). Also, you can define a threshold value to draw a line on the plot via the thr argument. Here is a sample usage for our case:
DDplot(my_data, discrim = 'ULI', k = 3, l = 1, u = 3, thr=0.1)It can be seen that items 30, 31 and 40 from our simulated dataset are below our 0.1 threshold value in terms of discrimination. Interestingly, items 30 and 31 are the most difficult items while item 40 is the easiest one. What a weirdo… :D
Conclusion
Examining item difficulty and item discrimination are important aspects of evaluating the psychometric properties of a measure. Item difficulty measures how easy or difficult each individual item is for respondents to answer correctly, while item discrimination measures the extent to which each item differentiates between participants who have high or low levels of the construct being measured.
In this blog post, we explored how to calculate item difficulty and item discrimination in R using an example dataset. We explained what each of these psychometric properties are, why they’re important, and how to interpret the results. We also discussed some limitations and considerations when examining these properties.
Overall, understanding and evaluating the psychometric properties of a measure can help ensure its reliability and validity, and inform decisions about item selection and revision.